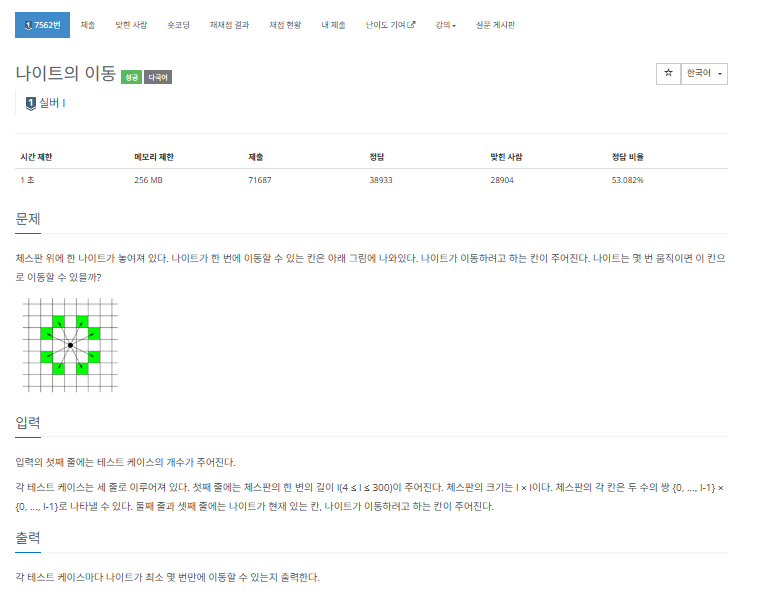
https://www.acmicpc.net/problem/7562
나이트의 이동
[DFS,BFS] 백준 7576번 토마토(C++)
[DFS,BFS] 백준 7576번 토마토(C++)
https://www.acmicpc.net/problem/7576 멋쟁이 토마토 토마토 내용은 쉽다1의 번짐이지 퉁퉁퉁퉁퉁사후르 같은거 기대하고 토마토그려달라햇는데토마토가 토마토를 먹는 그림이 나옴무서워 잡설은 그만
lee-soo.tistory.com
이 문제는 토마토 문제를 꼭 풀고 와야 된다
왜냐면 그 코드 위주로 수정해서 풀었거든
내용은 쉽다
어라
그냥...
나이트가 해당 체스판으로 가는 최소 움직임의 수를 구하면 되네?
예제하나를보면

8 * 8 체스판안에서
0,0 -> 7,0으로 가는 최단 경로의 수는?

이제 빨간색에서 파란색으로 이동하는 경로를 말하는 것이다
그렇다면?

아마 여러 경로가 있겠지만 최소 5번의 경우의 수가 나온다
이런식으로 자리를 찾는 것인데
우리가 토마토에서 dp를 어떻게 사용했나?
각 이동경로에서 갈 수 있는 곳마다 dp[i-1]+1을 해가면서 해당 위치의 점의 dp를업데이트 시켜놨었다
즉

나이트로 갈 수 있는 모든 경로를 정하고 그걸 bfs로 꾸준히 움직이면서 그 값에 그 이전값의 위치값(움직인 값) +1을 해주면서 업데이트 해 나가는 것이다

이렇게 계속 퍼져나가는 것이다( visited 하였으면 그 이전에 도착한거니까 그건제외 )
그리고 만약? 원하는 위치에 도달했다면 그 dp값을 출력해주고 return 해주는 것이다
#include <iostream>
#include <queue>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
queue<pair<int, int>> q;
bool visited[300][300];
int arr[300][300] = {0};
int dp[300][300];
int dx[8] = {2, 1, -2, 1, 2, -1, -2, -1};
int dy[8] = {1, 2, 1, -2, -1, 2, -1, -2};
void task(int n, int target_x, int target_y);
int main()
{
int m;
cin >> m;
while (m--)
{
int n;
int target_x, target_y, start_x, start_y;
cin >> n;
cin >> start_x >> start_y >> target_x >> target_y;
dp[start_x][start_y] = 0;
q.push(make_pair(start_x, start_y));
task(n, target_x, target_y);
q = queue<pair<int, int>>();
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
// 초기화
visited[i][j] = false;
arr[i][j] = 0;
dp[i][j] = 0;
}
}
}
}
void task(int n, int target_x, int target_y)
{
while (!q.empty())
{
if (visited[target_x][target_y])
{
cout << dp[target_x][target_y] << "\n";
return;
}
int x = q.front().first;
int y = q.front().second;
q.pop();
visited[x][y] = true;
// cout << "x : " << x << ", y : " << y << "\n";
for (int i = 0; i < 8; i++)
{
int nx = x + dx[i];
int ny = y + dy[i];
if (nx >= 0 && ny >= 0 && nx < n && ny < n)
{
if (!visited[nx][ny] && arr[nx][ny] == 0)
{
// cout << nx << " " << ny << "\n";
dp[nx][ny] = dp[nx - dx[i]][ny - dy[i]] + 1;
visited[nx][ny] = true;
arr[nx][ny] = 1;
q.push(make_pair(nx, ny));
}
}
}
}
}
우선 이 문제는 bfs로 풀었다. 그러면 각 움직일 수 있는 값들이 초기화 되어 퍼져나가는데
dfs로 할 경우, 움직일 수 있는 값이 정말 많아질 것이다. ( 가장 깊은 곳 까지 가야되는데 만약 100*100이면 거의 100*100을 모두 돎 )
그 안에서 최솟값을 또 찾으려면 힘들것이다.
또한 토마토에서 dx dy를 미리 적용하여 풀었었는데
이번에는 나이트의 움직임에 따라
int dx[8] = {2, 1, -2, 1, 2, -1, -2, -1};
int dy[8] = {1, 2, 1, -2, -1, 2, -1, -2};
총 8가지의 경우의수를 고려하여 정의해놓았다.
arr 배열을 넣은것이 보일텐데 이건 지금보니까 굳이 안넣어도 문제푸는덴 문제 없을 것 같다





